
分享:储气库生产管柱的气固冲蚀性能
储气库在天然气调峰和保障供气安全方面具有不可替代的作用及优势。多周期、强注、强采的生产模式使储气库管柱承受温度、压力等循环载荷的耦合作用,在服役过程中发生冲蚀减薄甚至失效,这对管柱完整性及安全运行管理提出了巨大挑战[1-2]。
为了提高储气库单井注采能力、降低建库成本,目前国内部分储气库注采井采用小型压裂改造完井,但这类井在采气时可能出现支撑剂及地层砂回流现象,因此管柱的耐冲蚀性能也成为储气库井筒设计需要考虑的主要因素之一[3-4]。
针对井下管柱的冲蚀问题,国内外研究者做了大量的研究工作。ALAM等[5]认为管道发生流动冲蚀的主要原因是严重的塑性变形和材料脱落,在较高的流速下,犁削和微切削会引起二次流动冲蚀。VIEIRA等[6]发现在相同的冲击角度下,颗粒冲击速率越高,流动冲蚀速率越大。在相同的粒子冲击速率下,冲击角度越低,流动冲蚀速率越高,其最大角在15°~40°。目前,计算流体力学(CFD)被广泛应用于颗粒冲蚀研究中[7],冲蚀计算一般分为三个步骤:求解流场、跟踪流域中的颗粒、基于颗粒的冲蚀模型计算冲蚀速率等信息[8-9]。ZENG等[10]通过计算流体力学和离散元素法(CFD-DEM),发现冲击频率、冲击速率和冲击角度是影响流动冲蚀行为的主要因素,随着颗粒球度的增加,流动冲蚀速率先降低后升高。
王志远等[2]总结了储气库管柱冲蚀理论及预测技术,进一步明确了现有研究的不足及冲蚀预测在储气库管柱设计方面的重要性。练章华等[11-12]、邹洪岚等[13]、安杰[14]通过研究,初步掌握了井下管柱冲蚀问题的损伤机理及规律;刘铭钢等[15]对全管柱的流体状态进行了模拟研究,并间接分析了冲蚀风险;何祖清等[16]采用传统临界冲蚀流速方法对文37储气库的冲蚀规律及极限注采量进行了分析。
国内外相关研究表明,气固冲蚀受到流动工况、颗粒属性、基体材料属性等多种因素的影响,基本明确了冲蚀特征随流动参数的变化规律,但在冲蚀风险的评估方面仍多采用传统的临界冲蚀流速,缺少冲蚀风险与生产参数的直接关联性研究,同时在实际生产工况下特定材料的冲蚀风险评估方面仍有不足,不能直接指导气田或储气库的生产过程。
作者针对长庆油田榆3×储气库的生产工况,建立了冲蚀预测模型,对N80管柱的耐冲蚀性能进行分析,并确定了生产管柱的临界生产参数,为储气库管柱设计及安全运行提供了理论支撑。
1. 榆3×储气库基本情况
榆3×储气库气藏平均埋深为2 955 m,原始地层平均压力为27.7 MPa,地层平均温度为90.0 ℃,气藏温度与埋深呈线性关系,储气库下限压力为14.4 MPa,上限压力等于地层压力,为27.7 MPa。采用?114.3 mm×7.37 mm规格油管完井,其井身结构如图1所示。
在榆3×储气库注气过程中,管柱内的介质以天然气为主,基本不含固体颗粒;在采气过程中,介质以天然气(含少量轻烃组分,相对密度0.6)、颗粒(支撑剂、地层砂)为主,可能引起管柱的冲蚀,因此作者主要针对储气库的采气过程进行分析。榆3×储气库气藏压力为14.4~27.7 MPa,井口油压控制在6.7~18.2 MPa,一个采气周期为120 d;对该规格管柱而言,极限采气量(20 ℃,1.01×105 Pa)为102.6×104 m3/d,实际采气量在45.1×104 ~98.1×104 m3/d。榆3×储气库预计出砂量为12 kg/d,平均砂粒直径为0.59 mm。
2. 冲蚀预测模型
采用Fluent软件构建冲蚀预测模型,主要包括:流动模型、离散相模型(DPM)以及冲蚀模型。模型以天然气与固体颗粒为介质,将天然气视为连续相,将固体颗粒视为离散相。
2.1 数学模型
2.1.1 流动模型
天然气为可压缩流体,其流动模型基于Navier-Stokes方程,包括连续方程及动量方程(不考虑温度变化)。
连续方程:
|
|
(1) |
动量方程:
|
|
(2) |
式中:ρ为流体密度,kg/m3;u为流体流速,m/s;p为流体压力,Pa;μ为流体的动力黏度,Pa·s;g为重力加速度,m/s2。
选择Realizable k-ε模型作为湍流模型。
2.1.2 离散相模型
采用离散相模型模拟颗粒的运动过程,颗粒运动由牛顿第二定律决定,其控制方程为
|
|
(3) |
式中:mp为颗粒质量,kg;up为颗粒运动速率,m/s;F为颗粒受力,N。FD、FB、FP、FVM分别为流场对颗粒的拖曳力、浮力、压力梯度力、虚拟质量力。由于流场中固体颗粒的尺寸较小,并且连续相和离散相之间的密度差较大,马格努斯力、巴赛特力、Saffman升力相对于拖曳力很小,可以忽略不计。
为了准确预测颗粒轨迹,在离散相模型中加入回弹模型,并用恢复系数描述碰撞特性,本模型中采用了常用的Forder恢复系数,如式(4)~(5)所示。
|
|
(4) |
|
|
(5) |
式中:en为法向的恢复系数;et为切向的恢复系数;θ为入射角。
2.1.3 冲蚀模型
影响颗粒冲蚀的因素很多,如颗粒属性、颗粒的冲击速率和冲击角度、流动参数及流道的几何形状等。本冲蚀模型选用了综合性较高的Oka模型[17-18],如式(6)~(7)所示。
|
|
(6) |
|
|
(7) |
式中:ve为冲蚀速率,kg/(m2·s);HV为基体材料的维氏硬度,GPa;dc为颗粒直径,μm;uc为颗粒的冲击速率,m/s;F(α)为颗粒侵入角函数。k0、k1、k2、k3、n1、n2为Oka模型参数。
2.2 管道模型
依据油管规格?114.3 mm×7.37 mm,选取长度为2 m的管段构建几何模型,如图2(a)所示。榆3×储气库的最大井眼曲率位于井深3 000 m处,为0.059 6(°)/ m,相对于长度而言,其弯曲角度可忽略,即管段为平直状态。通过改变管段倾斜角度实现造斜段不同位置井筒的冲蚀模拟,如图2(b)所示。
计算域网格采用非结构六面体网格,网格总数为35.75万。为保证能够准确捕捉近壁区的流场特性,采用O型网格进行模拟,第一层边界层厚度设置0.000 05 mm,如图3所示。
2.3 边界条件
入口处采用流速作为边界条件,出口处采用压力作为边界条件。压力-流速耦合采用Coupled算法,动量、湍动能和湍流耗散率的离散均采用二阶迎风格式,压力的离散采用二阶差分格式。
2.4 物性参数
2.4.1 基体材料属性
油管材料为N80钢,其硬度为6.37 GPa,泊松比为0.29,杨氏模量为211 GPa,密度为7 850 kg/m3。
2.4.2 颗粒属性
榆3×储气库预计出砂量为12 kg/d,主要为压裂用陶粒,平均砂粒直径为0.59 mm。依据SY/T 5108-2018《压裂支撑剂性能指标及测试推荐方法》选用不同粒径的陶粒配制颗粒。颗粒粒径的选取范围依据现场实际监测结果确定,平均颗粒直径与现场保持一致,为0.59 mm,颗粒粒径与质量分布见表1,颗粒球度为1,密度为2 650 kg/m3。
| 粒径/mm | 质量分数/% | 粒径/mm | 质量分数/% |
|---|---|---|---|
| 0.43 | 14 | 0.59 | 6 |
| 0.64 | 42 | 0.89 | 18 |
| 0.85 | 14 | 1.19 | 6 |
2.5 模拟工况
依据榆3×储气库的采气工况,探索管柱冲蚀速率随工况参数的变化规律,依据压力及理想气体状态方程计算得到介质流速,选取的典型模拟工况见表2。
| 工况 | 压力/MPa | 采气量(20 ℃,1.01×105 Pa)/(104 m3·d-1) | 流速/(m·s-1) | 重力方向 |
|---|---|---|---|---|
| 工况1 | 27.7 | 102.6 | 6.90 | 垂直于流向 |
| 工况2 | 17.9 | 102.6 | 10.12 | 垂直于流向 |
| 工况3 | 14.4 | 102.6 | 12.61 | 垂直于流向 |
| 工况4 | 14.4 | 73.9 | 9.21 | 垂直于流向 |
| 工况5 | 14.4 | 45.1 | 5.54 | 垂直于流向 |
| 工况6 | 14.4 | 102.6 | 12.61 | 与流向呈135°夹角 |
| 工况7 | 14.4 | 102.6 | 12.61 | 与流向呈157.5°夹角 |
| 工况8 | 14.4 | 102.6 | 12.61 | 与流向呈112.5°夹角 |
| 工况9 | 14.4 | 102.6 | 12.61 | 与流向相反 |
3. 模拟结果与分析
图4为工况3下模拟结果。由模拟结果可知,管内的压力从入口到出口递减,如图4(a)所示;管道中心流速最大值为16.2 m/s,靠近管壁处流速为1.16 m/s,如图4(b)所示;受重力影响,颗粒沿流向逐步往重力方向移动,直至撞击壁面产生冲蚀后反弹流出,如图4(c)所示;管壁冲蚀位置分布在管道下部(重力方向),冲蚀位置与颗粒集中沉积位置一致,如图4(d)所示。由图4(e)可以看出,在管道径向,冲蚀速率基本呈现对称分布。由图4(f)可以看出,最大冲蚀速率位于距入口1.81 m处,最大冲蚀速率为4.93×10-8 kg/(m2·s),即0.20 mm/a。
3.1 冲蚀速率的影响因素
3.1.1 采气工况
图5为采气工况对最大冲蚀速率的影响。在工况1~3下,采气量保持不变,压力增加,最大冲蚀速率减小,如图5(a)所示。这是因为一方面,随着压力增加,气体密度增加,若采气量保持不变,气体流速降低,颗粒沉积到壁面的速率减小;另一方面,气体密度的增加提高了气体对颗粒的携带能力,最大冲蚀速率与采气压力呈现出非线性的关系。在工况3~5下,压力保持不变,采气量的增加,管内介质流速增加,最大冲蚀速率增加,如图5(b)所示。结合Oka计算公式可以看出,冲蚀速率与颗粒冲击速率呈非线性正相关,而颗粒冲击速率直接受流体流速的影响。
3.1.2 管道倾角
图6为管道倾斜角度对最大冲蚀速率的影响。由图6可见,随着油管倾斜角度的增加,最大冲蚀速率减小,水平状态时,最大冲蚀速率要大于其他倾斜或垂直状态。由于重力在垂直于介质流动方向的分量减小,因此撞击壁面的颗粒冲击速率与颗粒数量均减少。
3.1.3 颗粒属性
为进一步探索出砂量、颗粒直径、颗粒球度等属性对冲蚀的影响规律,以表2中的工况3为基准,对不同颗粒属性条件下管道的冲蚀进行了模拟,颗粒参数设置及模拟结果分别见表3及图7。
| 平均颗粒直径/mm | 颗粒流量/(kg·d-1) | 颗粒球度 | 最大冲蚀速率/(kg·m-2·s-1) | 最大冲蚀速率/(mm·a-1) |
|---|---|---|---|---|
| 0.59 | 12 | 1.0 | 4.93×10-8 | 0.20 |
| 0.59 | 4 | 1.0 | 1.64×10-8 | 0.07 |
| 0.59 | 1 | 1.0 | 4.11×10-9 | 0.02 |
| 0.43 | 12 | 1.0 | 3.71×10-8 | 0.15 |
| 0.85 | 12 | 1.0 | 5.94×10-8 | 0.24 |
| 1.19 | 12 | 1.0 | 7.71×10-8 | 0.31 |
| 0.59 | 12 | 0.9 | 5.31×10-8 | 0.21 |
| 0.59 | 12 | 0.7 | 6.16×10-8 | 0.25 |
| 0.59 | 12 | 0.5 | 7.15×10-8 | 0.29 |
| 0.59 | 12 | 0.3 | 8.29×10-8 | 0.33 |
从模拟结果可以看出,随着出砂量的增加,最大冲蚀速率呈线性增大;随着颗粒直径的增加,最大冲蚀速率基本呈线性增大;随着颗粒球度的增加,最大冲蚀速率基本呈线性减小,这说明球形颗粒导致的冲蚀弱于非球形颗粒,与相关研究结论一致。
3.2 N80钢的临界生产参数
参考NACE SP0755-2018 Preparation,Installation,Analysis,and Interpretation of Corrosion Coupons in Oilfield Operations标准中腐蚀程度判据,见表4,确定N80钢的临界冲蚀速率。
| 腐蚀程度 | 均匀腐蚀速率/(mm·a-1) | 腐蚀程度 | 均匀腐蚀速率/(mm·a-1) |
|---|---|---|---|
| 低 | <0.025 | 高 | 0.13~0.25 |
| 中 | 0.025~0.12 | 严重 | >0.25 |
由于水平段管柱的冲蚀最为严重,以水平放置的管段为模拟对象,选取14.40、18.83、23.27、27.70 MPa采气压力,通过扩大采气量、出砂量的模拟工况,反推N80钢的临界生产参数。
图8(a)为不同采气压力下N80油管内壁冲蚀速率随采气量的变化规律。可以看出,在采气压力相同的情况下,冲蚀速率随采气量的增大呈现先增加后降低的趋势,当压力为14.40、18.83、23.27、27.70 MPa时最大冲蚀速率分别为0.056、0.056、0.055、0.053 mm/a。
为进一步明确冲蚀速率随出砂量的变化规律,在极限采气量(102.6×104 m3/d)下,对不同出砂量条件下的冲蚀速率进行了模拟,结果见图8(b)。可以看出,冲蚀速率均随出砂量的增加线性增加,但随着采气压力的提高,冲蚀速率增加速率减小。
基于表4中低、中、高及严重风险对应的临界冲蚀速率,建立了榆3×储气库N80油管的临界生产参数,如图9所示。在实际生产过程中,现场操作人员可以依据实时的生产工况实现油管冲蚀风险的评估,避免油管的冲蚀失效。
4. 结论
(1)在榆3×储气库预设采气量范围内(45.1×104~102.6×104 m3/d),最大冲蚀速率随采气量的增大而增大;采气压力的增加会降低管柱的冲蚀程度;冲蚀程度随出砂量的增加呈现线性增加趋势,颗粒直径的增大会导致冲蚀速率的增大,而颗粒球度的减小(颗粒越尖锐)会导致冲蚀速率的增大。
(2)建立了榆3×储气库N80油管在不同冲蚀风险程度下的临界生产参数图版,为储气库现场的安全生产及冲蚀风险评估提供了依据。
文章来源——材料与测试网





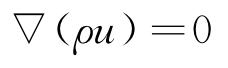
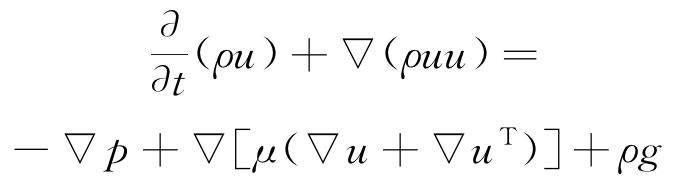
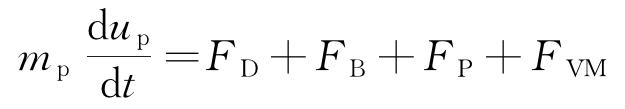
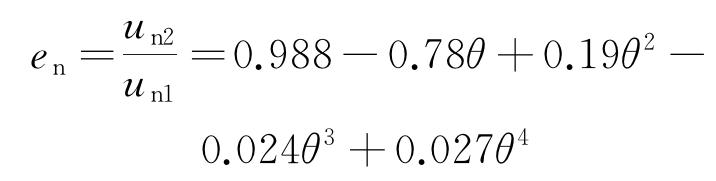
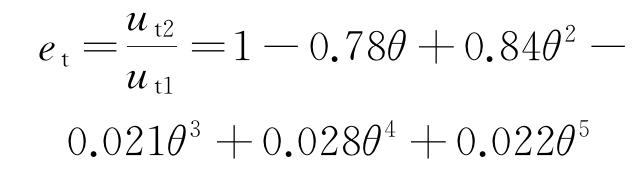
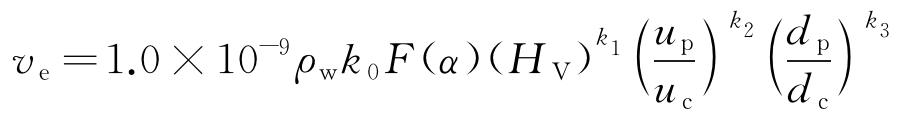
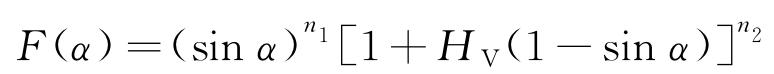









 浙公网安备 33042402000106号
浙公网安备 33042402000106号

