油气运输管道以钢质管道为主，但管道周围敷设环境复杂，管道受温度、湿度、紫外线、酸碱性影响势必会发生腐蚀，导致管壁变薄，甚至穿孔泄漏[1]。国内外学者针对腐蚀管道剩余强度进行了大量研究，如：基于断裂力学理论推导出用于计算腐蚀管道剩余强度的半经验公式NG-18[2]；基于有限元分析方法推导计算管道失效压力的PCORRC方法[3]，该方法相对于早期的公式降低了保守性；基于神经网络推算出用于计算腐蚀管道剩余强度的IPSO-BPNN算法；基于ASME-B31G腐蚀管道剩余强度评价方法改进的SY/T651-2009标准模型[4]。

由腐蚀管道剩余强度评价模型得到的预测结果与实际值仍存在偏差[1,3,5-7]。针对此类情况，孙宝财等[8-9]将BP神经网络与遗传算法相结合，建立了适用于腐蚀管道剩余强度预测的神经网络算法，该方法提升了模型的准确性，同时也使公式更加简洁。MOKHTARI等[10]运用理想化腐蚀形状的估算方法对PCORRC模型和DNV RP-F101模型进行修正，将复杂的腐蚀形状理想简化，使公式运用更加方便。以上研究在模型准确性和便捷性方面有所改善，但并未考虑腐蚀管道剩余强度评价模型中各项参数与腐蚀管道实际剩余强度的关联情况。因此，有学者提出了全概率的修正方法，且这一方法已逐步在纤维复合材料本构模型、纤维与混凝土界面力、黏土中悬臂梁挠度等工程中应用[11-13]。

作者拟采用全概率数学方法解决腐蚀管道剩余强度评价模型的不确定性问题。

1. 模型

1.1 剩余强度评价模型简介

为预测腐蚀管道剩余强度，建立了大量评价模型[1,4,8-9,14-15]。对于腐蚀管道剩余强度评价模型的选取，一般遵循评价模型的实际运用情况及其在研究中的分析频率[1,3,6,8,15]。表1为工程中常用的4个评价模型，其分别为DNV RP-F101、PCORRC、SY/T6151-2009、ASME B31G-2012。模型中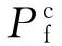为预测剩余强度（计算值），M为膨胀因子，D为管道直径，t为管道壁厚，L为管道腐蚀长度，d为管道腐蚀深度，σb为管材拉伸强度，σs为管材屈服强度。

早期的评价模型如DNV RP-F101并没有定义L/Dt2，但这并不代表其准确度不够。学者们之所以频繁使用此类型的评价模型是因为简单的膨胀因子定义使评价模型更加简洁，使用方便。作者将上述4种模型分别简称为D模型、P模型、S模型以及A模型。

1.2 数据收集

腐蚀管道剩余强度受很多因素影响，例如管道自身材料属性以及管道腐蚀情况[9,14,16]。然而，把所有影响因素都纳入考虑范围并不可行。所以作者选取了6个最为突出的影响因素作为重点参数，它们分别是：管道直径D、管道壁厚t、管道腐蚀深度d、管道腐蚀长度L、管材拉伸强度σb和管材屈服强度σs[17-18]。本研究以内压下单一腐蚀状况为主，将管道剩余强度定义为腐蚀管道实际爆破压力[19]。从文献[19-32]中共收集了237组试验数据用于模型计算。其中，管道直径范围为273.00~1 422.40 mm，管道壁厚范围为4.37~22.90 mm，管道腐蚀深度范围为1.54~18.55 mm，管道腐蚀长度范围为4.00~1 420.00 mm，管材拉伸强度范围为277.40~886.00 MPa，管材屈服强度范围为240.00~795.00 MPa，实际爆破压力范围为4.82~27.50 MPa。

1.3 模型因子

一般情况下，预测模型存在一定的理想化，会忽略实际情况。本研究中，通过定义模型因子来确定理想与实际之间的差距[33]。模型因子（ε）是实际值与预测值的比值，见式（1）。

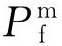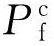式中：和分别为腐蚀管道剩余强度的试验值（实际值）和预测值。

从式（1）可以看出：ε越接近于1，预测值越接近实际值，表明此模型越准确；ε值远离1，表明试验值与预测值相差较大，模型存在较大不确定性。从实际角度分析，ε大于1说明模型是保守的，反之则是不安全的。

将收集的237个腐蚀管道剩余强度的试验值与4个模型的预测值进行比较，结果如图1所示。图中横纵坐标比值即为模型因子。从图1可知，模型因子呈两种类型的散点分布：一种是散乱的分散在45°线周围，如图1（c）所示；另一种是紧密分散在45°线下段部分，如图1（a，b，d）所示。

图 14种模型的模型因子

Figure 1.Model factors of four types of models

以模型因子为横坐标，其对应的频率为纵坐标，绘制4个模型的直方图，结果如图2所示。从直方图可以发现：D模型、P模型以及A模型的模型因子分别集中于1.33、1.38以及1.38附近，这3种评价模型相对保守；S模型的模型因子集中分布在0.85附近。从变异系数（COV）角度来看，4种模型的COV分别是0.29、0.29、0.37、0.29。综上所述，4种腐蚀管道剩余强度的评价模型都存在不确定性。作者将着重叙述D模型的详细修正方法，其余评价模型修正方法类似。

图 24种模型模型因子的直方图

Figure 2.Column diagrams of model factors from four types of models

从模型因子入手，对腐蚀管道剩余强度评价模型进行修正。模型因子仅反映计算值与实际值的差距，是一个随机变量，故模型因子的定义必须以随机性为前提[33-34]，与腐蚀管道剩余强度评价模型中的各参数没有相关性。通过Spearman法分析各项参数（D、t、d、L、σb、σs）与ε的相关性，包括相关性R和显著性P两项评判指标。图3为管道壁厚与D模型模型因子εD的Spearman分析。结果表明：其R为-0.233，P为0.00，这说明εD与管道壁厚呈负相关。对其余5个参数进行相同处理，所得结果列于表2中。结果表明，εD与6个参数（D、t、d、L、σb、σs）都有相关性，为了减小εD对6个参数的相关性，运用含有以上6个参数的回归方程f表示模型因子εD。此时的回归方程f不能完全等同于εD，因为f与实际的εD还存在一定的差距，为此引入残差因子ε*来修正f与实际εD之间的差值，详见式（2）。结合式（1）可以得到式（3）。回归方程f是εD系统部分，故残差因子ε*是随机的，与前文中的各参数没有相关性[12]。对于修正后模型，可以通过判断残差因子是否是随机变量评价其修正效果。故接下来的工作便是找到能系统表示εD的回归方程f。

图 3管道壁厚与D模型模型因子的Spearman相关性分析

Figure 3.Spearman correlation analysis of pipe wall thickness versus model factor of model D

2. 结果与讨论

2.1 回归方程拟合

随机挑选237组数据中的40组数据用于最后验证f和εD的准确性，剩下的197组数据用于回归方程的拟合。验证数据的挑选原则：数据挑选必须是随机的；数据应尽可能覆盖不同管道尺寸以及腐蚀情况。由前文可知εD与6个参数存在相关性，使用含有6个参数的回归方程进行系统拟合表示εD[11]。首先，确认εD与6个参数中每一个参数的相关函数类型即确定核心函数。

在确定核心函数时有很多工况会影响数据的集中，运用平均法处理εD使其散杂的数据集中，找到更好εD与各参数的真实函数关系。例如，当给定条件下管道腐蚀深度为9.00 mm时，有两组数据符合：D=914.40，t=16.40，d=9.00，σb=813.00，σs=739.00，εD=0.90；D=762.00，t=17.50，d=9.00，σb=557.00，σs=474.00，εD=1.21。

当d为9.00 mm时，εD平均值（记为εDave）为1.06，εDave=（0.90+1.21）/2=1.06。通过类似的做法得到参数d在各种工况下的εDave。对D模型中6个参数（D、t、d、L、σb、σs）做同样处理，通过此法找到已有工况对应的εDave，结果如图4所示。其中，空心圆点为平均模型因子εDave。从图4（f）可以看出，σs与εDave之间关系可以用幂函数来表示。其他参数均可用较高决定系数（R2）的非线性函数表示，为了回归方程的一致性，用幂函数或指数函数表示各参数的核心函数。

图 4D模型中各参数与平均模型因子的变化曲线

Figure 4.Curves of parameters with average model factors in mode D: (a) pipe diameter; (b) pipe wall thickness; (c) corrosion depth; (d) corrosion length; (e) tensile strength; (f) yield strength

各参数的核心函数如下所示：；εDave∝b2et；εDave∝b3ed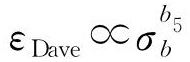；；；。其次，确认各参数核心函数后，将所有核心函数放在一个回归方程里，建立一个系数与核心函数的乘法模型f，以此表征ε随输入参数的系统变化，如式（4）所示。

式中：b0、b1、b2、b3、b4、b5、b6（统称为bi）为核心函数中的系数，均为未知数。接下来应先确认系数bi。运用SPSS23商业软件将前文所选的197组数据与εD依照式（4）进行多元线性拟合，计算出未知系数，结果详见表3。拟合回归方程的R2为0.62，拟合效果理想。D模型的ε可以表示为

由上文可知，残差因子ε*是一个随机量，与之前各参数没有相关性。使用前文用于验证的40组数据，对残差因子ε*进行相关性分析，残差因子ε*在各种工况下的值由（5）式计算得出。为方便对比，再次运用平均法得到平均残差因子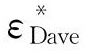。在图4中用实心黑点表示平均残差因子。由图4可见，实心黑点随机分布在1左右，与原参数的核心函数无关。Spearman相关性分析结果见表2。从表2中可以看出修正后的残差因子ε*相关系数R处于很低水平，显著系数P都大于0.05。从结果可以推测出，修正后的εD对6个参数的相关性大大降低。因此，可以说残差因子ε*是εD的随机部分。上述回归方法消除了εD对于参数的依赖性（相关性）。按类似的方法对P模型、S模型以及A模型进行修正，3个模型的未知系数见表3。三个评价模型的ε如下：

2.2 修正前后对比

通过表3中系数得到完整的回归方程，修正后模型公式如式（9）所示。

式中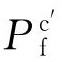：为修正后腐蚀管道剩余强度评价模型的预测值，f由式（4~8）所得。

为便于观测，以管道剩余强度实际值为横坐标、修正公式计算的管道剩余强度预测值为纵坐标，绘制散点图，如图5所示。修正后4个模型的各项指标列于表4中。由表4可知，D模型的模型因子平均值由修正前1.33降为修正后的1.09，变异系数由0.29降低到0.20；P模型的模型因子平均值由1.38降低到0.96，变异系数由0.29降低到0.21；S模型的模型因子平均值由0.85上升至1.06，变异系数由0.37降低至0.29；A模型的模型因子平均值由1.30降低至0.98，变异系数由0.29降低至0.21。

图 5修正后各模型的模型因子

Figure 5.Model factors of models after correction

对比图1和图5所示修正前后各模型的模型因子可知，修正前模型因子分布在45°直线下方位置，修正后模型因子密集分布在45°线上。这说明全概率法适用于修正腐蚀管道剩余强度评价模型，解决模型的不确定性问题。

3. 结论

运用全概率方法来修正腐蚀管道剩余强度评价模型，解决模型的不确定性。针对应用较为广泛的4个腐蚀管道剩余强度评价模型（DNV RP-F101、PCORRC、SY/T6151-2009和AMSE B30G-2012），通过237组腐蚀管道爆破试验数据获得模型因子（腐蚀管道剩余强度实际值与预测值的比值）。模型因子仅反映可预测性，是一个随机变量，与腐蚀管道剩余强度评价模型各参数无关。但经Spearman相关性分析发现：4个评价模型的模型因子与评价模型中的各参数（D、t、d、L、σb、σs）有关。

从237组数据中随机挑选197组试验数据建立多元回归方程f替代ε，减小ε与各参数的相关性。又利用剩余的40组数据验证回归后残差因子ε*的随机性。运用消除相关性校准方法后，4个评价模型的模型因子均值分别为1.09、0.96、1.06、0.98，变异系数分别为0.20、0.21、0.29、0.21。然而未去除相关性的原始评价模型的模型因子均值分别为1.33、1.38、0.85、1.30，变异系数分别为0.29、0.29、0.37、0.29。全概率修正方法适用于解决腐蚀管道剩余强度不确定性问题，并且提高了腐蚀管道剩余强度评价模型的可预测性和精度。

文章来源——材料与测试网